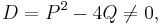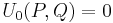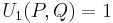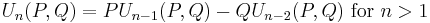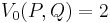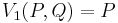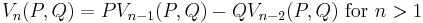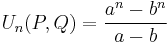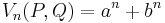Lucas pseudoprime

In number theory, the classes of Lucas pseudoprime and Fibonacci pseudoprime comprise sequences of composite integers that passes certain tests that all primes pass: in this case, criteria relative to some Lucas sequence.

Contents

Definition

Given two integer parameters P and Q which satisfy

D = P^2 - 4Q \neq 0 ,

the Lucas sequences of the first and second kind, Un(P,Q) and Vn(P,Q) respectively, are defined by the recurrence relations

U_0(P,Q)=0 \,
U_1(P,Q)=1 \,
U_n(P,Q)=PU_{n-1}(P,Q)-QU_{n-2}(P,Q) \mbox{ for }n>1 \,

and

V_0(P,Q)=2 \,
V_1(P,Q)=P \,
V_n(P,Q)=PV_{n-1}(P,Q)-QV_{n-2}(P,Q) \mbox{ for }n>1 \,

We can write

U_n(P,Q) = \frac{a^n-b^n}{a-b} \,
V_n(P,Q) = a^n %2B b^n \,

where a and b are roots of the auxiliary polynomial X2 - P X + Q, of discriminant D.

If p is an odd prime number then

Vp is congruent to P modulo p.

and if the Jacobi symbol

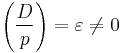\left(\frac{D}{p}\right) = \varepsilon \ne 0,

then p is a factor of Up-ε.

Lucas pseudoprimes

A Lucas pseudoprime[1] is a composite number n for which n is a factor of Un-ε. (Riesel adds the condition that the Jacobi symbol 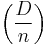\left(\frac{D}{n}\right) should be −1.)

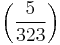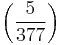In the specific case of the Fibonacci sequence, where P = 1, Q = -1 and D = 5, the first Lucas pseudoprimes are 323 and 377; \left(\frac{5}{323}\right) and \left(\frac{5}{377}\right) are both −1, the 324th Fibonacci number is a multiple of 323, and the 378th is a multiple of 377.

A strong Lucas pseudoprime is an odd composite number n with (n,D)=1, and n-ε=2rs with s odd, satisfying one of the conditions

n divides Us
n divides V2js

for some j < r. A strong Lucas pseudoprime is also a Lucas pseudoprime.

An extra strong Lucas pseudoprime is a strong Lucas pseudoprime for a set of parameters (P,Q) where Q = 1, satisfying one of slightly modified conditions

n divides Us and Vs is congruent to ±2 modulo n
n divides V2js

for some j < r. An extra strong Lucas pseudoprime is also a strong Lucas pseudoprime.

By combining a Lucas pseudoprime test with a Fermat primality test, say, to base 2, one can obtain very powerful probabilistic tests for primality. See the paper by Baillie and Wagstaff, and the books by Crandall and Riesel.

Fibonacci pseudoprimes

A Fibonacci pseudoprime is a composite number n for which

Vn is congruent to P modulo n

when Q = ±1.

A strong Fibonacci pseudoprime may be defined as a composite number which is a Fibonacci pseudoprime for all P. It follows (see Müller and Oswald) that in this case:

  1. An odd composite integer n is also a Carmichael number
  2. 2(pi + 1) | (n − 1) or 2(pi + 1) | (n − pi) for every prime pi dividing n.

The smallest example of a strong Fibonacci pseudoprime is 443372888629441, which has factors 17, 31, 41, 43, 89, 97, 167 and 331.

It is conjectured that there are no even Fibonacci pseudoprimes (see Somer).

See also

References

  1. ^ Robert Baillie; Samuel S. Wagstaff, Jr. (October 1980). "Lucas Pseudoprimes". Mathematics of Computation 35 (152): 1391–1417. http://mpqs.free.fr/LucasPseudoprimes.pdf. 
  • Richard E. Crandall; Carl Pomerance (2001). Prime numbers: A computational approach. Springer-Verlag. pp. 131–132. ISBN 0-387-94777-9. 
  • Hans Riesel (1994). Prime Numbers and Computer Methods for Factorization. Progress in Mathematics. 126 (2nd ed ed.). Birkhäuser. p. 130. ISBN 0-8176-3743-5. 
  • Müller, Winfried B. and Alan Oswald. "Generalized Fibonacci Pseudoprimes and Probable Primes." In G.E. Bergum et al., eds. Applications of Fibonacci Numbers. Volume 5. Dordrecht: Kluwer, 1993. 459-464.
  • Somer, Lawrence. "On Even Fibonacci Pseudoprimes." In G.E. Bergum et al., eds. Applications of Fibonacci Numbers. Volume 4. Dordrecht: Kluwer, 1991. 277-288.
  • Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. p. 45. ISBN 0-387-20860-7. 

External links